Group Work 08/29

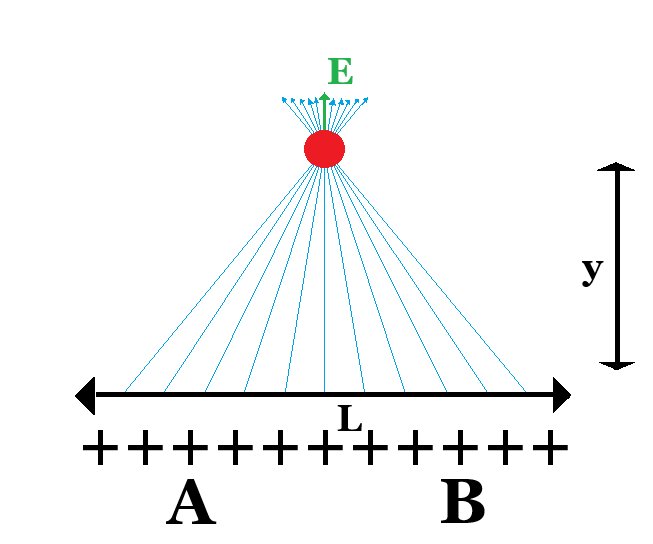
In this tutorial, we will calculate the electric field due to a long straight bar of charge at point P, which is on the bar's perpendicular bisector. While shown as eleven individual positive charges in the figure, in reality the charge is uniformly spread out along the bar. Additionally, the bar is essentially one-dimensional (along the x-axis) so the charge distribution can be described by λ = λ₀.

Draw vectors representing the electric field at point P due to the charges labeled A and B in the figure below. Your vectors should be quantitatively correct.
Answer: See figure below.
Determine the direction of the net electric field at point P (shown in red). Explain your answer.
Answer: Because of symmetry all the x components cancel and only the y components affect the particle.
To calculate the electric field at P we must evaluate the integral:

\[ \mathbf{E}(P)=\frac{1}{4\pi\varepsilon_{0}}\int \frac{\hat{\mathbf{R}}}{R^{2}}\, dq \]
Let's slowly work through this and get the integral set up correctly. How do you express the dq?
Answer:

\[ dq = λ₀\, dx \]
Your integral certainly needs limits. Two students at your table already have answers. One has \( \displaystyle \int_{0}^{L} \) while the other has \( \displaystyle \int_{\frac{L}{2}}^{-\frac{L}{2}} \). Are both of these answers correct? Will one make the calculation easier than the other? Explain your reasoning.
Answer:
Yes, both are correct. However, an integral from 0 to L/2 would be easiest to do, one only needs to double the result to account for the other half of the symmetry.
Determine \( r \), \( r\,' \), and \( \hat{R} \).
Answer:
- \(\mathbf r\) (position of \(P\)): \(\langle 0,\, r \rangle\)
- \(\mathbf r'\) (position of a source element at coordinate \(x\)): \(\langle x,\, 0 \rangle\)
- \(\mathbf R=\mathbf r-\mathbf r'\) (from source to \(P\)): \(\langle -x,\, r \rangle\)
- \(|\mathbf R|=\sqrt{x^{2}+r^{2}}\), \(\;\hat{\mathbf R}=\dfrac{\langle -x,\, r\rangle}{\sqrt{x^{2}+r^{2}}}\)
You should now be ready to write out the integral you need to solve so do it here. Explain any additional physics you included here which was not already accounted for in Questions #3-5.
Answer:
From parts 3 & the limits from 4 we have:

\[ \mathbf{E}(P) \;=\; \frac{λ₀}{4\pi\varepsilon_{0}}\; \int_{0}^{L/2} \frac{\hat{R}}{R^{2}}\, dx \]
Using the results from 5 we have:

\[ \mathbf{E}(P) \;=\; \frac{λ₀}{4\pi\varepsilon_{0}}\; \int_{0}^{L/2} \frac{\,r\,}{\left(x^{2}+r^{2}\right)^{3/2}}\, dx \]
Now multiplying the result by 2 from part 4 for we have:

\[ \mathbf{E}(P) \;=\; \frac{λ₀}{2\pi\, \varepsilon_{0}} \; \int_{0}^{L/2} \frac{\,r\,}{\left(x^{2}+r^{2}\right)^{3/2}}\, dx \]
Solve that integral for the electric field at point P due to the entire bar. Write your answer in terms of the total charge on the bar.
Answer:

Given (keeping only the surviving y–component by symmetry):
\[ \mathbf{E}(P) \;=\; \frac{\mathrm{λ₀}}{2\pi\,\varepsilon_{0}} \int_{0}^{L/2} \frac{\,r\,}{\left(x^{2}+r^{2}\right)^{3/2}}\, dx \quad\Rightarrow\quad \mathbf{E}(P)=E_y\,\hat{\mathbf y}. \]
Method 1 — Quick \(u\)-sub (pattern identity)
\[ \frac{d}{dx}\!\left(\frac{x}{\sqrt{x^{2}+r^{2}}}\right)=\frac{r^{2}}{(x^{2}+r^{2})^{3/2}} \;\Rightarrow\; \frac{r}{(x^{2}+r^{2})^{3/2}}\,dx=\frac{1}{r}\,du \quad\text{with}\quad u=\frac{x}{\sqrt{x^{2}+r^{2}}}. \] \[ x=0 \Rightarrow u=0,\qquad x=\frac{L}{2} \Rightarrow u=\frac{L/2}{\sqrt{(L/2)^{2}+r^{2}}}. \] \[ \boxed{\,E_y \;=\; \frac{\mathrm{λ₀}}{2\pi\,\varepsilon_{0}}\cdot\frac{1}{r}\, \left[\frac{x}{\sqrt{x^{2}+r^{2}}}\right]_{0}^{L/2} \;=\; \frac{\mathrm{λ₀}}{2\pi\,\varepsilon_{0}\,r}\, \frac{L/2}{\sqrt{r^{2}+(L/2)^{2}}}\,} \]
Method 2 — Trig substitution
\[ x=r\tan\theta,\quad dx=r\sec^{2}\theta\,d\theta,\quad (x^{2}+r^{2})^{3/2}=r^{3}\sec^{3}\theta \;\Rightarrow\; \frac{r}{(x^{2}+r^{2})^{3/2}}dx=\frac{1}{r}\cos\theta\,d\theta. \] \[ x=0 \Rightarrow \theta=0,\qquad x=L/2 \Rightarrow \theta=\arctan\!\left(\frac{L}{2r}\right). \] \[ \boxed{\,E_y \;=\; \frac{\mathrm{λ₀}}{2\pi\,\varepsilon_{0}}\cdot\frac{1}{r}\, \big[\sin\theta\big]_{0}^{\arctan(L/2r)} \;=\; \frac{\mathrm{λ₀}}{2\pi\,\varepsilon_{0}\,r}\, \sin\!\left(\arctan\!\frac{L}{2r}\right) \;=\; \frac{\mathrm{λ₀}}{2\pi\,\varepsilon_{0}\,r}\, \frac{L/2}{\sqrt{r^{2}+(L/2)^{2}}}\,} \]
Direction: \(\mathbf{E}(P)=E_y\,\hat{\mathbf y}\) (upward along +\(y\)).
What should the electric field be at point P if y >> L? Explain your reasoning. Verify that your answer in Question #7 agrees with this.
Answer:

Far-field result ( \( y \gg L \) ):
\[ \boxed{\,E(P)\;\approx\;\frac{1}{4\pi\,\varepsilon_{0}}\;\frac{λ₀\,L}{r^{2}}\,},\quad \text{direction: } +\hat{\mathbf y}. \]
Reasoning: In the far field, the finite rod behaves like a point charge with total charge \(Q=\lambda L = A0\,L\) located near the origin. By symmetry, x-components cancel and y-components add, and each element is at distance \(\approx y\), giving the point-charge form \(kQ/r^{2}\). Equivalently, from the exact expression replace \(\sqrt{r^{2}+(L/2)^{2}}\) by \(r\) when \(r\gg L\).
What should the electric field be at point P if y << L? Explain your reasoning. Verify that your answer in Question #7 agrees with this.
Answer:

Near-field result ( \( y \ll L \) ):
\[ \boxed{\,E(P)\;\approx\;\frac{1}{2\pi\,\varepsilon_{0}}\;\frac{λ₀}{r}\,},\quad \text{direction: } +\hat{\mathbf y}. \]
Reasoning: Near the midpoint and far from the ends, the finite rod behaves like an infinite line charge; end effects are negligible. Thus \(E=\lambda/(2\pi\varepsilon_{0}r)\) with \(\lambda =λ₀\). (Equivalently, take the \(L\to\infty\) limit of the exact expression.)